・遠くのものはコントラストが弱くなる
・遠くのものの形は省略する
など「距離」と「コントラスト」や「距離」と「形」を
結びつけて考えている人は多いと思います
では「コントラスト」と「形(シルエット)」を
結びつけて考えている人はどれくらいいるでしょうか?
遠景や近景などの距離感の描き分けに対して
何を根拠に描き分けたらいいかわからず
納得するまで手を動かすしかないと悩んでいる方は
この記事を読めば
「距離」「階調」「シルエット」を関連づけて
考えることができるようになり
距離感と描き込み具合を対応さることができるようになる
ヒントになるのではないかと思います
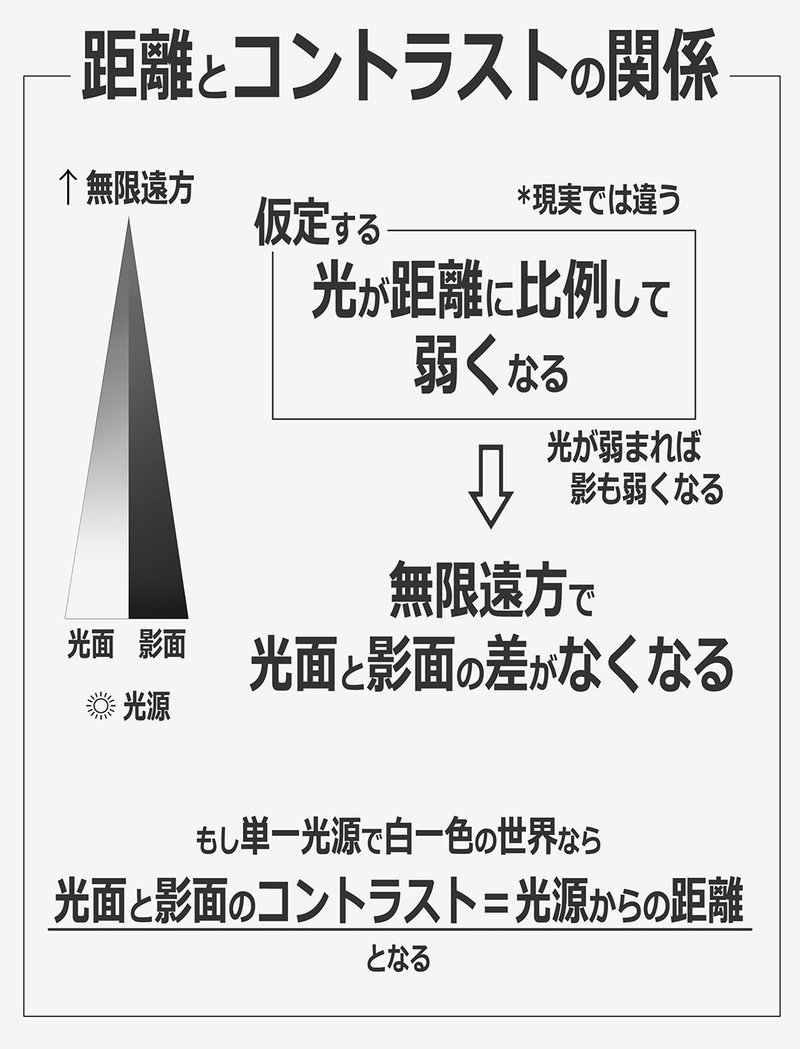
距離とコントラスト(明暗差)の関係
現実では違いますが
光が距離に比例して弱くなると仮定した場合
光は光源から遠くに行くほど弱くなり
光が弱くなれば影も弱くなるので
光と影は無限遠方で明暗差がつかなくなります
ここで、もし白一色の世界ならば
「光と影の明暗差(コントラスト)」=「光源からの距離」となります
「遠景」のコントラストが決まれば、「中景」「近景」のコントラストも決まる
もし観測者の立ち位置と遠景が決まれば
中景、近景のコントラストの範囲も決まります
中景のコントラストは
遠景のコントラストより強くなりますし
近景のコントラストより弱くなります
(これを地上の太陽光の下でも成り立つとします)
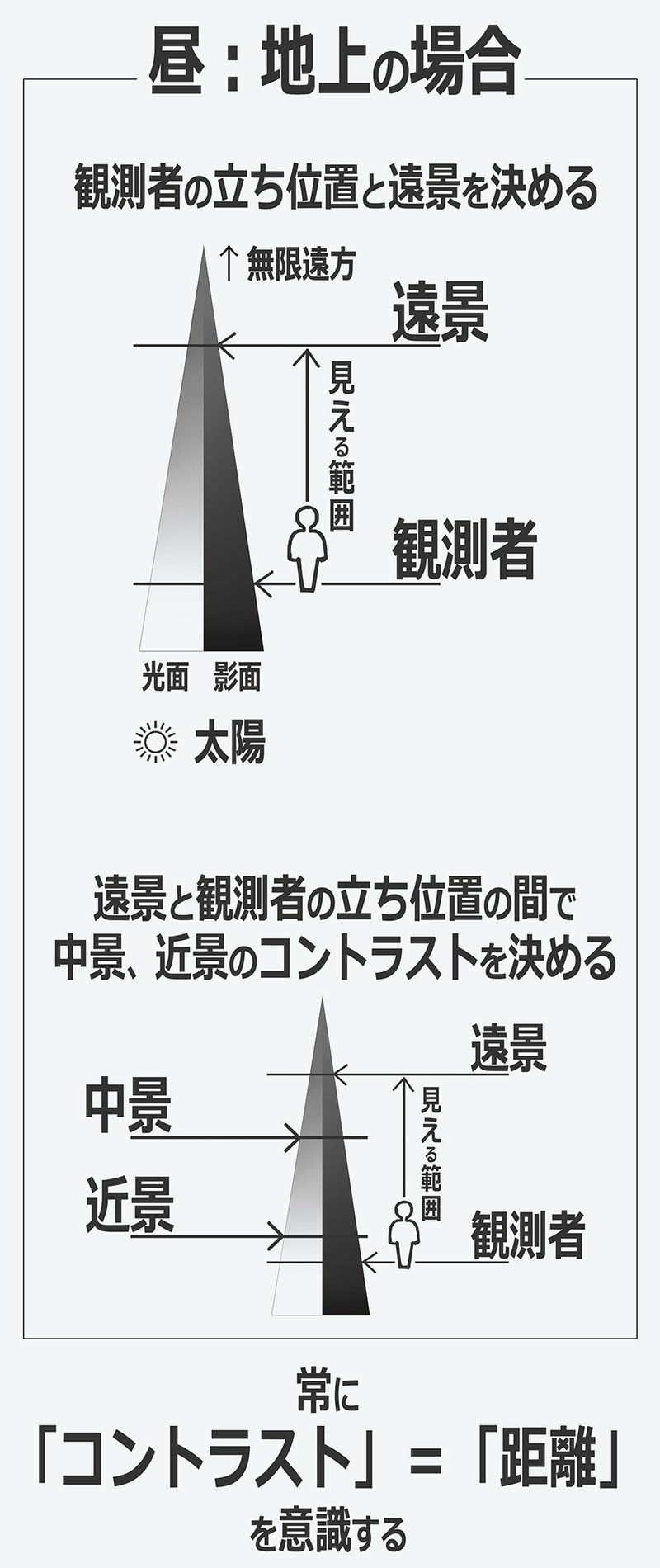
つまり明暗のコントラストが
観測者からの距離を表していると言えます
絵としての画面内で
適切な距離に適切なコントラストが対応していないと
ちぐはぐなものになってしまいます
「距離」=「コントラスト」を「距離」=「使える色幅」で考える
近景、中景、遠景のそれぞれで使える色幅は
それぞれの光面の色から影面の色までの間の色になります
(光面が一番明るく、影面が一番暗くなるからです)
この色幅をグラデーションで示したものが右下の図になります
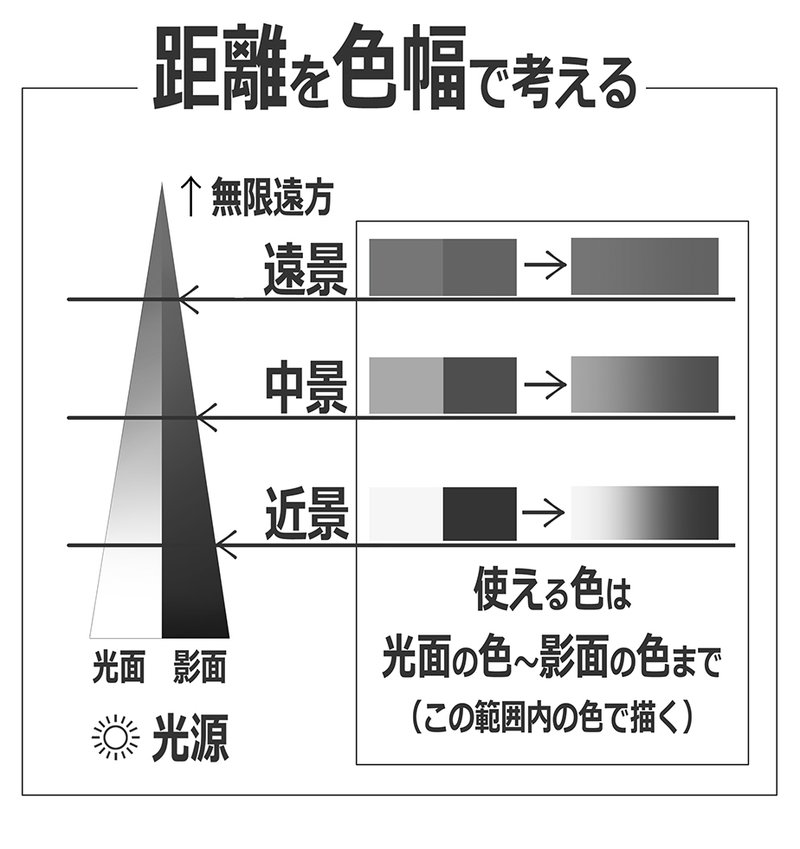
遠景のグラデーションはベタ塗りに見えないでしょうか?
中景のグラデーションに関しても
しっかりとした明暗差があるにしては
それほど色幅の広いグラデーションには見えないと思います
このことからわかるように
明暗境界部分にむやみに中間色を入れたりボカしたりしてしまうと
明暗の視認性が下がってしまうため
立体が弱く見えてしまうので注意が必要です
「距離」=「コントラスト」を「距離」=「使える階調数」で考える
近景、中景、遠景のそれぞれで使える色幅は
それぞれの光面の色から影面の色までの間の色になります
(光面が一番明るく、影面が一番暗くなるからです)
この色幅をいくつかの階調で示したものが右下の図になります
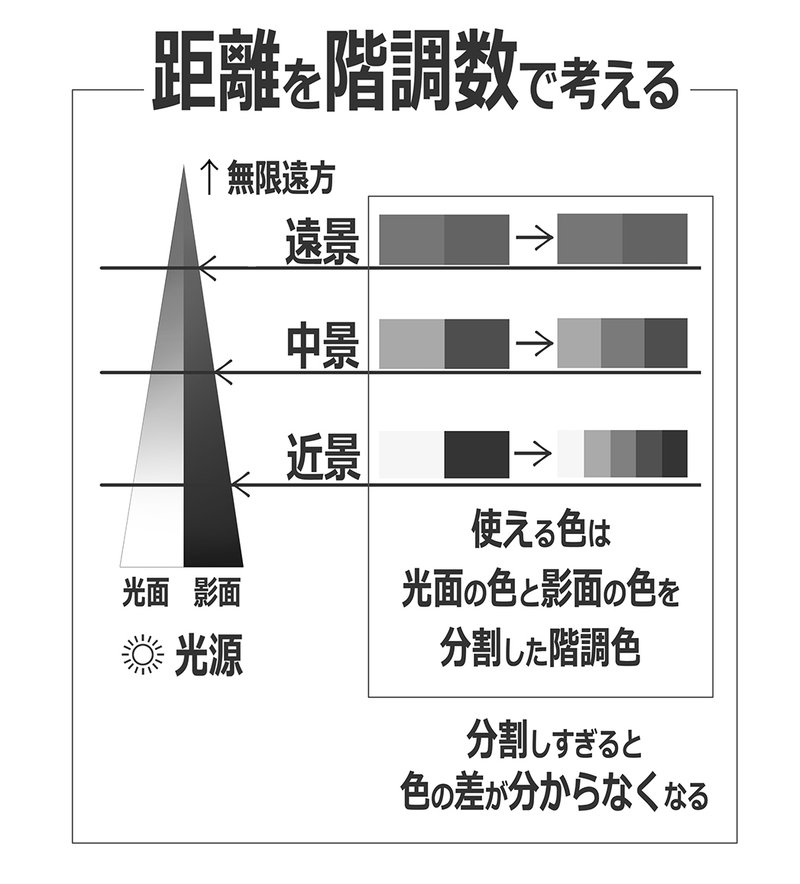
この階調で分けたものと上のグラデーションをかけたものは
同じ色幅なのにぱっと見の印象が全然違います
同じ色幅でも階調で分けたものかグラデーションかで
メリハリが違ってくるので
意識して使い分けないと見づらい絵になってしまいます
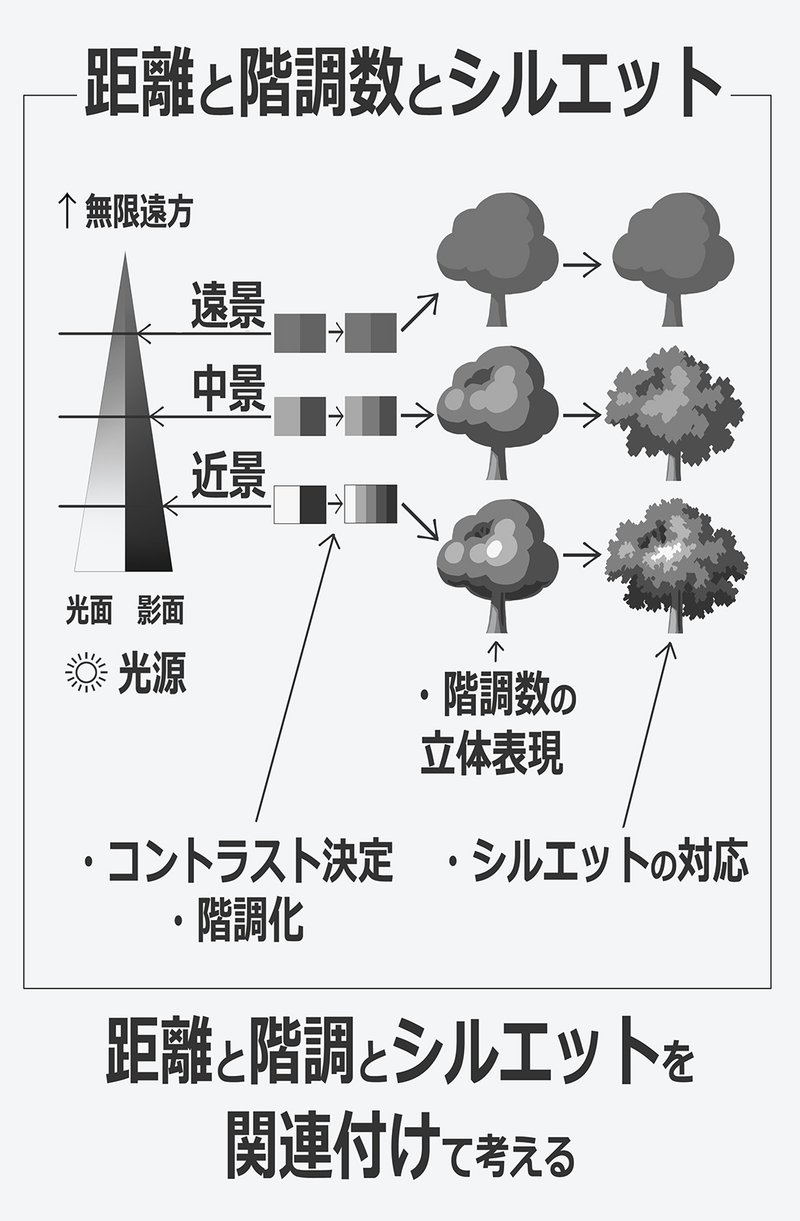
「距離」と「階調数」に「シルエット」を対応させる
光面の色、影面の色、ハイライト、反射光など
表現しなければいけない明暗だけでも3階調では足りません
光と影の中間色などを考えだしたらキリがありません
絵にするには、それらの情報を取捨選択して
まとめる必要があります
では、どのようにして絵として必要な情報を選択するのか?
というと距離と階調数を対応させて考えるのが簡単だと思います
・遠景は遠くてよく見えないので「光面」「影面」の2階調
・中景は遠景よりよく見えるので「光面」「影面」に加えて
「ハイライト」か「(地面か空からの)反射光」の3階調
・近景は、それらに加えて中間色などを使った5階調くらいとします
(階調数を増やしすぎるとグラデーションと同じように
メリハリが弱くなります)
下の図の上の段に
同じシルエットで階調数を変えたものを載せています
距離感の違いを十分表現できているのがわかると思います
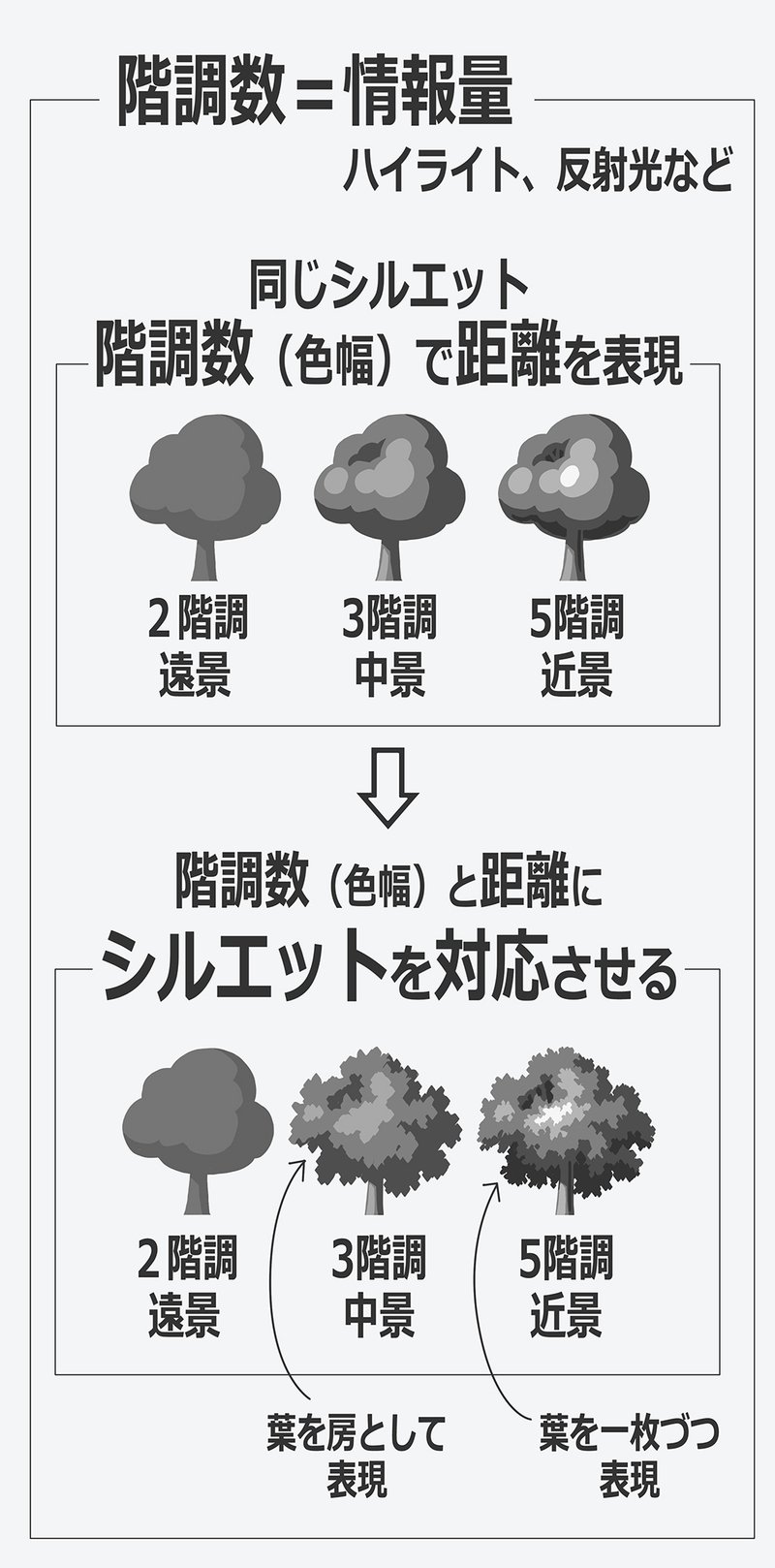
上図の下の段では
近景ほど見える情報量(階調数)が多いことから
形もよく見えると考えて
中景では葉を房(塊)として意識しています
近景では1枚ずつ葉の向きを意識したタッチで表現しています
まとめ
なんの根拠もなく
自分が納得するまで手を動かしている人には
一度「距離」「階調」「シルエット」を関連させて考えて
距離感と描き込み具合を対応させてみることをすすめます
上にある、まとめの図を簡易的に模写してみてはいかがでしょうか?
一度これらの関連性を体験しておけば
仮に遠景しか描かない場合や近景しか描かない場合であっても
自分の中でしっかりした距離感と描き込み具合を
コントロールできるようになると思います




